发布人:繁体字网(www.fantiz5.com) 发布时间:2016-02-21 07:30:00
| 试题原文 |
|
解:(1)原曲线方程可化简得: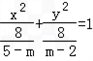 由题意,曲线C是焦点在x轴点上的椭圆可得: 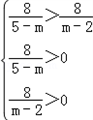 , ,解得: 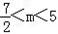 。 。(2)证明:由已知直线代入椭圆方程化简得:(2k2+1)x2+16kx+24=0, △=32(2k2-3)>0, 解得: 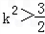 由韦达定理得:  ①, ①,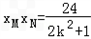 ,② ,②设N(xN,kxN+4),M(xM,kxM+4),G(xG,1), MB方程为: 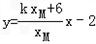 , ,则 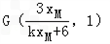 , ,∴ 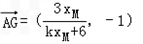 , ,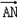 =(xN,kxN+2), =(xN,kxN+2),欲证A,G,N三点共线,只需证 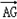 , ,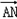 共线 共线即 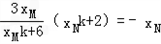 成立, 成立,化简得:(3k+k)xMxN=-6(xM+xN) 将①②代入可得等式成立,则A,G,N三点共线得证。 |
经过对同学们试题原文答题和答案批改分析后,可以看出该题目“已知曲线C:(5-m)x2+(m-2)y2=8(m∈R)。(1)若曲线C是焦点在x轴点上的..”的主要目的是检查您对于考点“高中直线与椭圆方程的应用”相关知识的理解。有关该知识点的概要说明可查看:“高中直线与椭圆方程的应用”。