发布人:繁体字网(www.fantiz5.com) 发布时间:2015-05-13 07:30:00
| 试题原文 |
|
| 解:(1)连结PC、PA、PB,过P点作PH⊥x轴,垂足为H, ∵⊙P与y轴相切于点C(0,1), ∴PC⊥y轴, ∵P点在反比例函数  的图象上, 的图象上, ∴P点坐标为(k,1), ∴PA=PC=k.在Rt△APH中,AH=  , , ∴OA=OH-AH=k-  , ,∴A(k-  ,0), ,0),∵由⊙P交x轴于A、B两点,且PH⊥AB,由垂径定理可知,PH垂直平分AB, ∴OB=OA+2AH=k-  +2 +2 =k+ =k+ , , ∴B(k+  ,0), ,0),故过A、B两点的抛物线的对称轴为PH所在的直线解析式为x=k, 可设该抛物线解析式为y=a  +h, +h,又抛物线过C(0,1),B(k+ 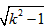 ,0), ,0),得:  解得a=1,h=1-  , ,∴抛物线解析式为y=  , ,(2)由(1)知抛物线顶点D坐标为(k,1-  ) ) ∴DH=  -1, -1,若四边形ADBP为菱形,则必有PH=DH, ∵PH=1, ∴ 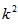 -1=1, -1=1,又∵k>1, ∴k=  , ,∴当k取  时,PD与AB互相垂直平分,则四边形ADBP为菱形。 时,PD与AB互相垂直平分,则四边形ADBP为菱形。 |
|
经过对同学们试题原文答题和答案批改分析后,可以看出该题目“已知圆P的圆心在反比例函数图象上,并与x轴相交于A、B两点,且始..”的主要目的是检查您对于考点“初中求二次函数的解析式及二次函数的应用”相关知识的理解。有关该知识点的概要说明可查看:“初中求二次函数的解析式及二次函数的应用”。