发布人:繁体字网(www.fantiz5.com) 发布时间:2016-03-11 07:30:00
| 试题原文 |
|
解:(1)①设cn=an+bn,则 ﹣( ﹣(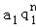 + +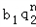 )( )( + + ) )=a1b1  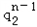 (q1﹣q2)2 (q1﹣q2)2当q1=q2时,对任意的n∈N,n≥2,  =c n+1 c n﹣1恒成立, =c n+1 c n﹣1恒成立,故{an+bn}为等比数列; ∴Sn= 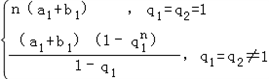 当q1≠q2时,对任意的n∈N,n≥2,  ≠c n+1 c n﹣1,{an+bn}不是等比数列. ≠c n+1 c n﹣1,{an+bn}不是等比数列.②设dn=anbn,对于任意n∈N*, 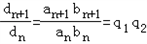 ,{anbn}是等比数列. ,{anbn}是等比数列. Sn= 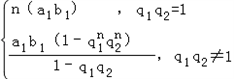 (2)设{an},{bn}均为等差数列,公差分别为d1,d2,则: ①{an+bn}为等差数列;Sn=(a1+b1)n+ 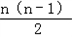 (d1+d2) (d1+d2)②当d1与d2至少有一个为0时,{anbn}是等差数列, 若d1=0,Sn=a1b1n+ 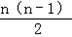 a1d2; a1d2;若d2=0,Sn=a1b1n+  b1d1. b1d1.③当d1与d2都不为0时,{anbn}一定不是等差数列. |
经过对同学们试题原文答题和答案批改分析后,可以看出该题目“设{an}和{bn}均为无穷数列.(1)若{an}和{bn}均为等比数列,试研究..”的主要目的是检查您对于考点“高中等比数列的通项公式”相关知识的理解。有关该知识点的概要说明可查看:“高中等比数列的通项公式”。