发布人：繁体字网（www.fantiz5.com） 发布时间：2016-02-06 07:30:00
| 试题原文 |
|
解：∵椭圆方程为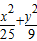 =1， ∴a2=25，可得a=5 ∵△MF1F2中，N、O分别为MF1和MF1F2的中点 ∴|ON|=  |MF2| ∵点P在椭圆 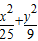 =1上，可得|MF1|+|MF2|=2a=10 ∴|MF2|=10-|MF1|=8， 由此可得|ON|= 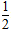 |MF2|= ×8=4 故选：B  |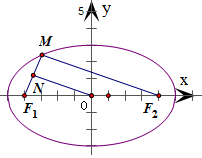
经过对同学们试题原文答题和答案批改分析后，可以看出该题目“已知椭圆方程x225+y29=1，椭圆上点M到该椭圆一个焦点F1的距离是..”的主要目的是检查您对于考点“高中椭圆的性质（顶点、范围、对称性、离心率）”相关知识的理解。有关该知识点的概要说明可查看：“高中椭圆的性质（顶点、范围、对称性、离心率）”。