发布人:繁体字网(www.fantiz5.com) 发布时间:2016-01-16 07:30:00
| 试题原文 |
|
解:(Ⅰ)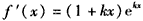 ,f′(0)=1,f(0)=0, ,f′(0)=1,f(0)=0,曲线y=f(x)在点(0,f(0))处的切线方程为y=x。 (Ⅱ)由 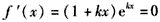 ,得 ,得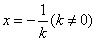 , ,若k>0,则当 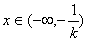 时,f′(x)<0,函数f(x)单调递减; 时,f′(x)<0,函数f(x)单调递减;当 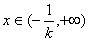 时,f′(x)>0,函数f(x)单调递增; 时,f′(x)>0,函数f(x)单调递增;若k<0,则当 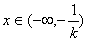 时,f′(x)>0,函数f(x)单调递增; 时,f′(x)>0,函数f(x)单调递增;当 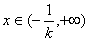 时,f′(x)<0,函数f(x)单调递减; 时,f′(x)<0,函数f(x)单调递减;(Ⅲ)由(Ⅱ)知,若k>0,则当且仅当 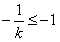 ,即k≤1时,函数f(x)在(-1,1)内单调递增; ,即k≤1时,函数f(x)在(-1,1)内单调递增;若k<0,则当且仅当 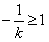 ,即k≥-1时,函数f(x)在(-1,1)内单调递增; ,即k≥-1时,函数f(x)在(-1,1)内单调递增;综上可知,函数f(x)在区间(-1,1)内单调递增时,k的取值范围是[-1,0)∪(0,1]。 |
经过对同学们试题原文答题和答案批改分析后,可以看出该题目“设函数f(x)=xekx(k≠0),(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方..”的主要目的是检查您对于考点“高中导数的概念及其几何意义”相关知识的理解。有关该知识点的概要说明可查看:“高中导数的概念及其几何意义”。